Higher-order Langevin Algorithms

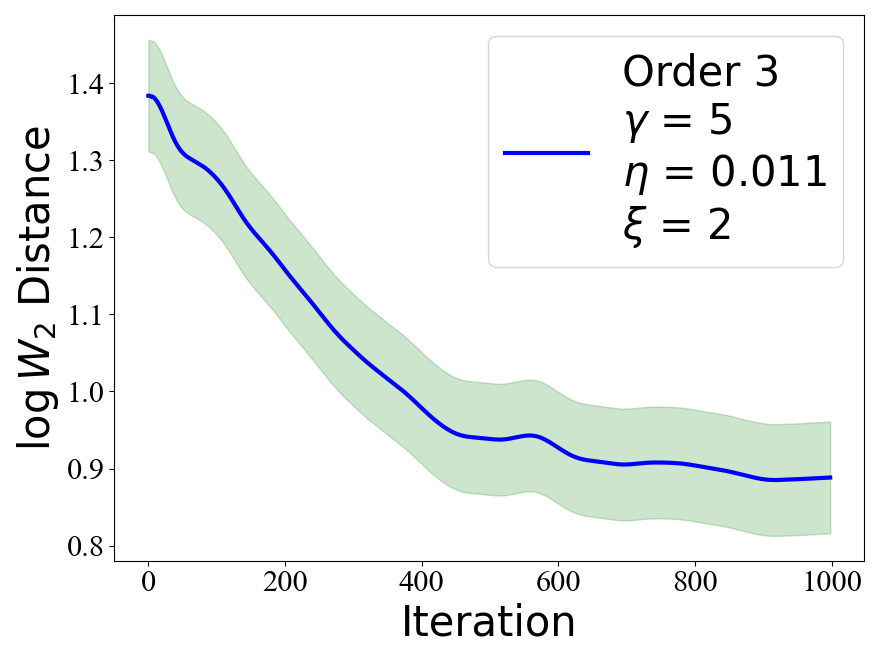
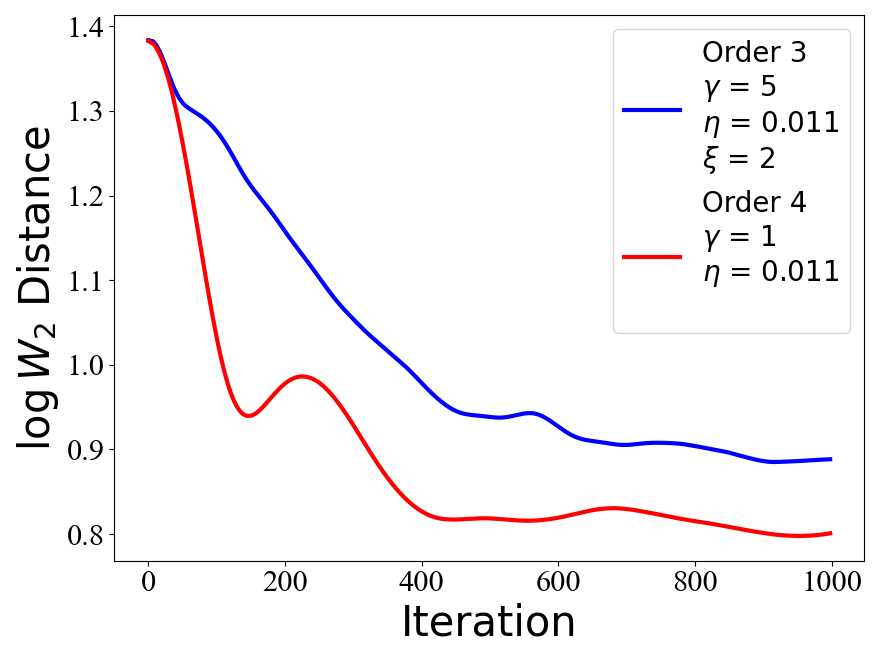
Langevin algorithms are popular Markov chain Monte Carlo (MCMC) methods for large-scale sampling problems that often arise in data science. We propose Monte Carlo algorithms based on \(P\)-th order Langevin dynamics for any \(P\geq 3\). Our design of \(P\)-th order Langevin Monte Carlo (LMC) algorithms is by combining splitting and accurate integration methods. We obtain Wasserstein convergence guarantees for sampling from distributions with log-concave and smooth densities. Specifically, the mixing time of the \(P\)-th order LMC algorithm scales as \(O\left(d^{\frac{1}{\mathcal{R}}}/\epsilon^{\frac{1}{2\mathcal{R}}} \right)\) for \(\mathcal{R}=4\cdot\mathbf{1}_{\{ P=3\}}+ (2P-1)\cdot\mathbf{1}_{\{ P\geq 4\}}\), which have better dependence on the dimension and the accuracy level as \(P\) grows. Numerical experiments illustrate the efficiency of our proposed algorithms.