Implementation of Gradient Descent (GD) and Stochastic Gradient Descent (SGD)

Gradient Descent

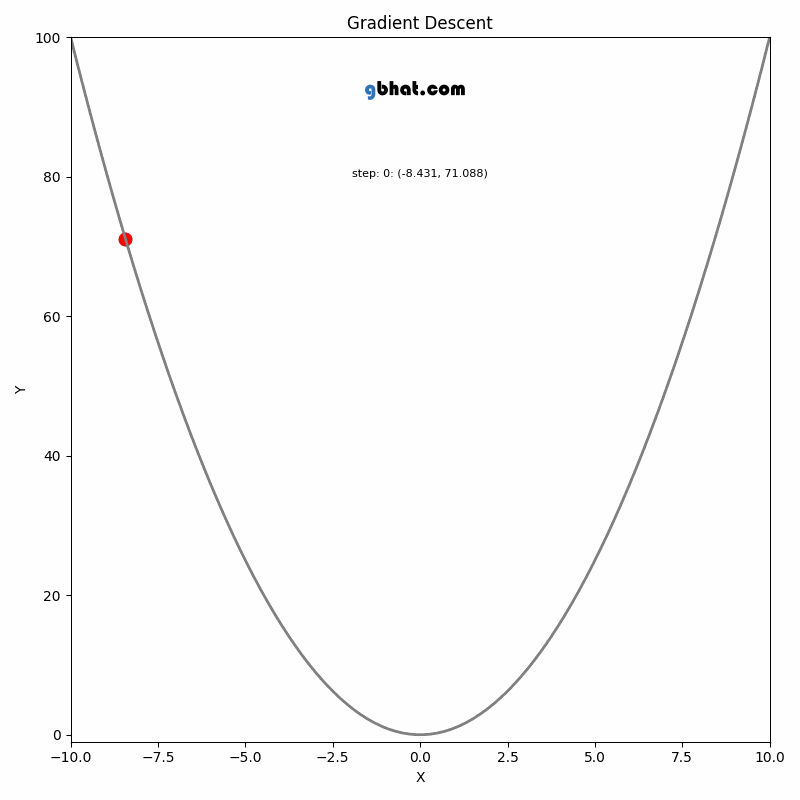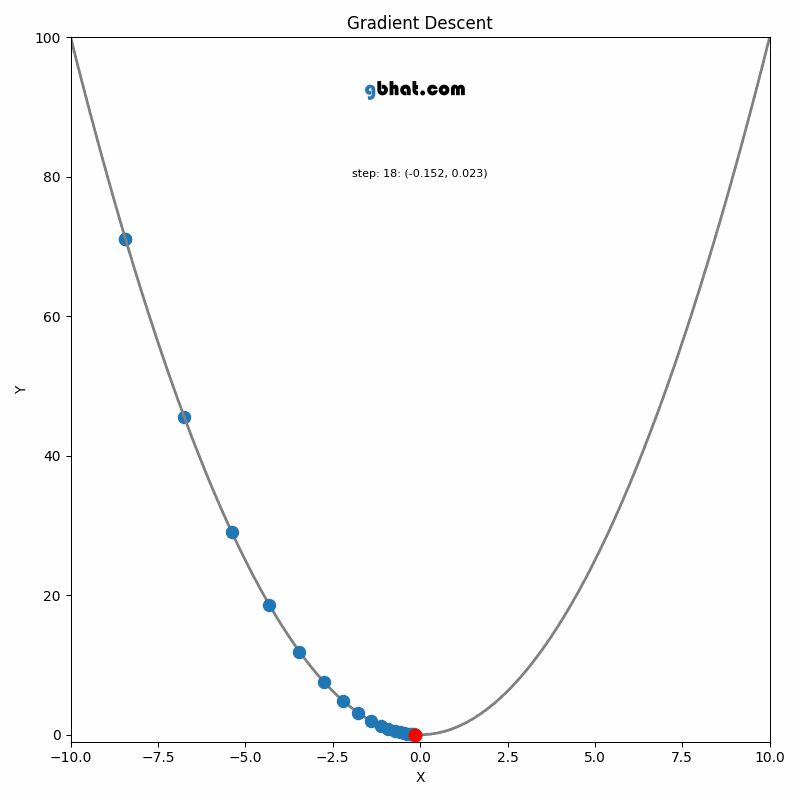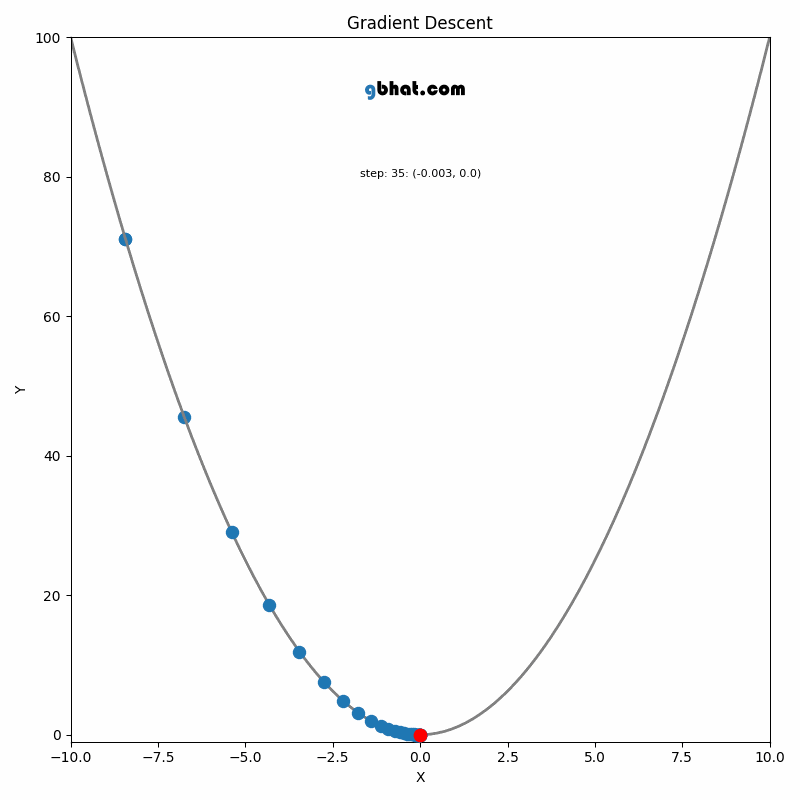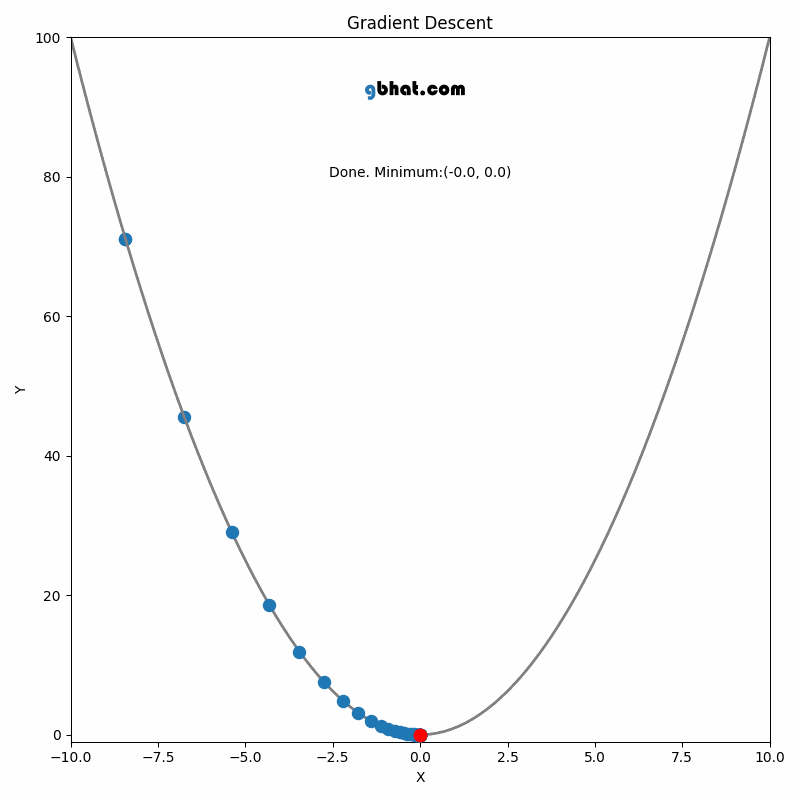
GIF Credit: gbhat.com

Gradient Descent is an optimization algorithm used to minimize the cost function. The cost function \(f(\beta)\) measures how well a model with parameters \(\beta\) fits the data. The goal is to find the values of \(\beta\) that minimize this cost function. In terms of the iterative method, we want to find \(\beta_{k+1}\) and \(\beta_k\) such that \(f(\beta_{k+1})<f(\beta_k)\).

For a small change in \(\beta\), we can approximate \(f(\beta)\) using Taylor series expansion
\[f(\beta_{k+1})=f(\beta_k +\Delta\beta_k)\approx f(\beta_k)+\nabla f(\beta_k)^T \Delta \beta_k+\text{higher-order terms}\]

The update rule for vanilla gradient descent is given by:

\[ \beta_{k+1} = \beta_k - \eta \nabla f(\beta_k) \]

Where:

• \(\beta_k\) is the current estimate of the parameters at iteration \(k\).
• \(\eta\) is the learning rate, a small positive scalar that controls the step size.
• \(\nabla f(\beta_k)\) is the gradient of the cost function \(f\) with respect to \(\beta\) at the current point \(\beta_k\).

The update rule comes from the idea of moving the parameter vector \(\beta\) in the direction that decreases the cost function the most.

1. Gradient: The gradient \(\nabla f(\beta_k)\) represents the direction and magnitude of the steepest ascent of the function \(f\) at the point \(\beta_k\). Since we want to minimize the function, we move in the opposite direction of the gradient.

2. Step Size: The term \(\eta \nabla f(\beta_k)\) scales the gradient by the learning rate \(\eta\), determining how far we move in that direction. If \(\eta\) is too large, the algorithm may overshoot the minimum; if it’s too small, the convergence will be slow.

3. Iterative Update: Starting from an initial guess \(\beta_0\), we repeatedly apply the update rule until the algorithm converges, meaning that the changes in \(\beta_k\) become negligible, and \(\beta_k\) is close to the optimal value \(\beta^*\).

Stochastic Gradient Descent (SGD)

Stochastic Gradient Descent is a variation of the vanilla gradient descent. Instead of computing the gradient using the entire dataset, SGD updates the parameters using only a single data point or a small batch of data points at each iteration. The later one we call it mini batch SGD.

Suppose our cost function is defined as the average over a dataset of size \(n\):

\[ f(\beta) = \frac{1}{n} \sum_{i=1}^{n} f_i(\beta) \]

Where \(f_i(\beta)\) represents the contribution of the \(i\)-th data point to the total cost function. The gradient of the cost function with respect to \(\beta\) is:

\[ \nabla f(\beta) = \frac{1}{n} \sum_{i=1}^{n} \nabla f_i(\beta) \]

Vanilla gradient descent would update the parameters as:

\[ \beta_{k+1} = \beta_k - \eta \nabla f(\beta_k) \]

Instead of using the entire dataset to compute the gradient, SGD approximates the gradient by using only a single data point (or a small batch). The update rule for SGD is:

\[ \beta_{k+1} = \beta_k - \eta \nabla f_{i_k}(\beta_k) \]

Where:

• \(i_k\) is the index of a randomly selected data point at iteration \(k\).
• \(\nabla f_{i_k}(\beta_k)\) is the gradient of the cost function with respect to the parameter \(\beta_k\), evaluated only at the data point indexed by \(i_k\).

Implementation

Let’s imagine a hypothetical scenario, Walmart Inc. wants to explore their business in a new twon. They want to have their store in location so that the total distance of the store from all the houses in the neighborhood is the smallest possible. If they have the data of \(n\) houses with corresponding coordinates of the houses, return the optimized location for the store.

The Euclidean distance between two points \((x_1,y_1)\) and \((x_2,y_2)\) is given by
\[d=\sqrt{(x_1-x_2)^2+(y_1-y_2)}\]

Assume that \(P=(x,y)\) is the coordinate of Walmart. So for a total of \(n\) such points the total distance \(D\) from the point \(P\) is a function of two variable \(x\) and \(y\) of the following form

\[D=f(x,y)=\sum_{i=1}^{n}\sqrt{(x-x_i)^2+(y-y_i)^2}\]

import numpy as np
import matplotlib.pyplot as plt
from mpl_toolkits.mplot3d import Axes3D

def f(x,y, c, d):
    return np.sqrt((x-c)**2+(y-d)**2)

x = np.linspace(-10,10, 400)
y = np.linspace(-10,10, 400)
x, y = np.meshgrid(x,y)

c, d = 0,0

z = f(x, y, c, d)

fig = plt.figure()
ax = fig.add_subplot(111, projection ='3d')
ax.plot_surface(x, y, z, cmap= 'viridis')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.gca().set_facecolor('#f4f4f4') 
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.savefig('sgd.png')
plt.show()

all we need to do is to minimize the function \(f(x,y)\) and to do that we need to calculate the gradient vector which is the partial derivative of \(f(x,y)\) with respect to \(x\) and \(y\). So,

\[\begin{align*} \frac{\partial f}{\partial x}& = \sum_{i=1}^{n} \frac{x-x_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}}\\ \frac{\partial f}{\partial y}& = \sum_{i=1}^{n} \frac{y-y_i}{\sqrt{(x-x_i)^2+(y-y_i)^2}}\\ & \\ \implies \nabla f(x,y) &= \begin{bmatrix}\frac{\partial f}{\partial x}\\\frac{\partial f}{\partial y}\end{bmatrix} \end{align*}\]

Then the algorithm

\[\begin{align*} \begin{bmatrix}x_{i+1}\\y_{i+1}\end{bmatrix}&= \begin{bmatrix}x_{i}\\y_{i}\end{bmatrix} - \eta_i \begin{bmatrix}\frac{\partial f}{\partial x}|_{x_i}\\\frac{\partial f}{\partial y}|_{y_i}\end{bmatrix} \end{align*}\]

where, the \(\eta\) is the step size or learning rate that scales the size of the move towards the opposite of the gradient direction.

Next, how do we control the numerical stability of the algorithm? We need to decrease the step size at each iteration which. This is called the rate of decay. We also need a termination factor or tolerance level that determines if we can stop the iteration. Sometimes, for a deep down convex function, the process oscillates back and forth around a range of values. In this case, applying a damping factor increases the chance for a smooth convergence.

Gradient Descent (GD)

import numpy as np
import matplotlib.pyplot as plt
import math

class GDdistanceMin:
    def __init__(self, step_size=1, decay_rate=0.99, tolerance=1e-7, damping_rate=0.75, points=[]):
        self.step_size = step_size
        self.decay_rate = decay_rate
        self.tolerance = tolerance
        self.damping_rate = damping_rate
        self.points = points
        self.x = sum(x for x, y in points) / len(points)  # Initialization
        self.y = sum(y for x, y in points) / len(points)  # Initialization
        self.x_updates = []
        self.y_updates = []

    def _partial_derivative_x(self, x, y):
        grad_x = 0
        for xi, yi in self.points:
            if x != xi or y != yi:
                grad_x += (x - xi) / math.sqrt((x - xi)**2 + (y - yi)**2)
        return grad_x

    def _partial_derivative_y(self, x, y):
        grad_y = 0
        for xi, yi in self.points:
            if x != xi or y != yi:
                grad_y += (y - yi) / math.sqrt((x - xi)**2 + (y - yi)**2)
        return grad_y

    def gradient_descent(self):
        dx, dy = 0, 0
        while self.step_size > self.tolerance:
            dx = self._partial_derivative_x(self.x, self.y) + self.damping_rate * dx 
            dy = self._partial_derivative_y(self.x, self.y) + self.damping_rate * dy 
            self.x -= self.step_size * dx 
            self.x_updates.append(self.x)
            self.y -= self.step_size * dy 
            self.y_updates.append(self.y)
            self.step_size *= self.decay_rate
        return (self.x, self.y)

def f(x, y, c, d):
    return np.sqrt((x - c)**2 + (y - d)**2)

# Define points
points = [(1, 3), (-2, 4), (3, 4), (-2, 1), (9, 2), (-5, 2)]
gd_min = GDdistanceMin(points=points)
min_pt = gd_min.gradient_descent()
xs = gd_min.x_updates
ys = gd_min.y_updates
print("Minimum point:", min_pt)

c, d = min_pt

# Create a grid for plotting
x = np.linspace(-10, 10, 400)
y = np.linspace(-10, 10, 400)
x_grid, y_grid = np.meshgrid(x, y)
z = f(x_grid, y_grid, c, d)

# Calculate z values for the updates
zs = [f(xi, yi, c, d) for xi, yi in zip(xs, ys)]

# Plotting
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
ax.plot_surface(x_grid, y_grid, z, cmap='viridis', alpha=0.6)
ax.scatter(xs, ys, zs, color='red', s=50, label="Updates", marker='o')
ax.set_xlabel('X')
ax.set_ylabel('Y')
ax.set_zlabel('Z')
plt.gca().set_facecolor('#f4f4f4') 
plt.gcf().patch.set_facecolor('#f4f4f4')
plt.show()

Minimum point: (0.9999997458022071, 2.9999999769909707)

Testing

Share on

Share

Tweet

You may also like